4 標本調査の基礎知識1

LSAでは，さまざまな国や地域の学校を対象に学力調査を行います。もっとも，すべての学校を調査していたのでは莫大な予算と時間がかかってしまいますから，通常は一部の学校を取り出して調査を行います。全体を知るために，一部（標本）を取り出して調査する手法のことを，標本調査と呼びます。ここでは本書を読む上で，最低限必要な標本調査の基礎知識を説明します。なお，標本調査に関する詳しい説明は，社会調査の入門書^[1]を読むようにしてください。

4.1 母集団と標本

最初に，母集団と標本という言葉について説明します。分析の対象となる集団すべてのことを「母集団」と呼びます。たとえば日本の小学6年生の学力が知りたいのであれば，母集団は「日本の学校に通う小学6年生全員」になるでしょう。

ただ冒頭でも述べたように，母集団をすべて調べるのはあまりに予算と時間がかかりすぎるので，普通は母集団の一部を取り出して調査を行います。この取り出した一部を「標本」と呼び，母集団から標本を取り出すことを「抽出」と言います。また，標本から母集団の特徴を予測することを「推定」と呼びます（図 4.1）。

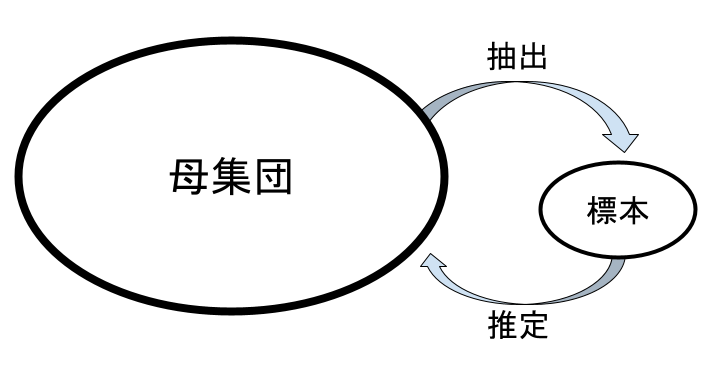
冒頭の例で言うと，日本全国の小学6年生（＝母集団）の学力を知るために，母集団から「抽出」した一部の学校の小学6年生（＝標本）にテストを行います。そして標本平均が60点だったら，母平均も60点（あるいはそれに近い値）だろうと「推定」するわけです。

母集団と標本に関連して，他にもいくつか重要な用語があります。まず，「標本」に含まれる対象の数のことを標本サイズ（あるいはサンプルサイズ）と呼びます。 3000人を抽出した場合，サンプルサイズ3000ということになります。よく似た用語として，標本数（サンプル数）という言葉がありますが，これは取り出した標本の数です。普通，社会調査では標本を1回しか取り出さない（≒アンケートは1回しかしない）ので，サンプル数は1になります。

次に，平均や分散といった統計量¹は，母集団のそれと標本のそれを区別します。一般に母集団のそれは母を頭につけて，母平均・母分散といった表現をします。また，母集団の統計量を，母数と呼ぶことがあります。母数に対し，標本の平均は標本平均というふうに標本を付けて区別します。

一般に母数は未知ですから，手元の標本から推測することになります。母平均と標本平均は近い値になることが期待できますが，完全に一致するとはかぎりません。ですから標本調査において，「日本のPISAの数学リテラシーの標本平均が530点である」は適切な表現ですが，「日本のPISAの数学リテラシーの母平均が530点である」は正しいとはかぎりません。

図 4.1 の中でもっとも重要な作業が抽出です。抽出の方法が間違えていたら，母数を推定することは困難だったり，あるいは不可能だったりします。たとえば日本に住む人（＝母集団）が好きな野球の球団を知りたいのに，博多駅前を通りかかった人（＝標本）に調査をするのは間違っています。おそらく福岡ソフトバンクホークスがもっとも好きな球団になってしまうでしょう。母集団から標本を取り出すときは，できるだけ標本が母集団の縮図になるように努力する必要があります。

4.2 標本抽出の方法

母集団から標本を抽出する方法には，さまざまな手法がありますが， LSAを知る上で重要な方法には，次のものがあります。

単純な無作為抽出
村落抽出法
多段抽出法
層化抽出法

それぞれ簡単に説明すると，単純な無作為抽出（Simple Random Sampling: SRS）とは，どの対象も同じ確率で選ばれる可能性がある抽出法のことです。あまり現実的ではありませんが，全国の小学生の名簿を用意して，そこからサイコロを振ってランダムに対象者を選ぶというのが，単純な無作為抽出になります。サイコロという偶然に任せて対象者を決めるので，母集団と標本の特徴は，よく似通ったものになることが想定できます。

ただ，SRSがLSAで採用されることはまずありません。まず，全国の小学生の名簿を用意するのが大変な手間です。仮に用意できたとしても，SRSでは離島の学校に調査対象者が1名いるといった極端な状況が発生する可能性があります。たった1名を調べるために遠隔地へ出向くのは費用対効果という点から見て問題があります。さらに，一つの学校に1名しか調査を受ける子どもがいないと，仮にその学校の学力が高かったとして，それが調査対象になった子どもの特性なのか，それとも学校の指導法に要因があるのか分析することが困難になります。

そこで登場するのが，対象となる子どもが通う学校名のリストを用意して，そこから学校をランダムに選び，対象になった学校の児童生徒全員を調査するというものです。日本全国の小学6年生の学力を知りたいのであれば，まず日本の小学校の一覧を用意し，サイコロを振って調査対象となる学校を決めます。そして選ばれた学校のすべての児童に学力調査を行うのです。これを村落抽出法（Cluster Sampling）と呼びます。村落抽出法は，全国学力・学習状況調査の保護者に対する調査や経年比較分析調査で利用されています²。

調査対象となった学校から，さらに児童生徒を抽出するという方法もあります。サイコロを振って調査対象となる学校を選んだ後で，その学校に対して小学6年生の名簿を提出してもらいます。その上で，個々の学校の名簿についてサイコロを振って，調査の対象となる児童を決めるわけです。これを多段抽出法（Multistage Sampling）と呼びます。多段抽出法はPISAで採用されており，まず学校を選び，続いて各学校から生徒を抽出する多段抽出法（学校・生徒という二段階の抽出を行うので，とくに二段抽出と呼びます）が使われています。

村落抽出法や多段抽出法は対象者を効率よく選択できるという利点がある一方で，精度が落ちるという欠点があります。一般に，同じ学校に通う子どもは似た特徴を持つと考えられます。同じ地域で育ち，同じような指導を受けてきたわけですから，学力や考え方・行動に似た部分が出てくるだろう・・・ということです。そのため村落抽出法や多段抽出法は，SRSに比べて得られる情報量が少なくなります。極端な例ですが，仮に各学校の子どもの学力がまったく同じ（A校は全員50点，B校は全員40点・・・）だったとしたら， A校から10人選んでも全体の推測にはあまり役立たず， SRSで母集団から10人選んだ方が圧倒的に良いということになります。

精度が落ちるという欠点に対処するため，村落抽出法や多段抽出法を層化抽出法（Stratified Sampling）という方法と組み合わせることがよく行われます。この場合，層化村落抽出法／層化多段抽出法といった呼び方がされます。

層化とは学力に影響を与えると思われる要因で各学校をグループ（層）にまとめておき，その層の中から学校を抽出するという方法です。一例として，都市部かそうでないかで学力実態が大きく変わることが想定できます。であれば，事前に学校を都市部かそうでないかで二つのグループに分けておき，それぞれから学校を抽出すれば，標本には必ず都市部／それ以外の学校が混ざるので，何も考慮しなかった場合よりも精度が上がることが期待できます。

いろいろと述べてきましたが，実のところ，LSAを分析する際にさまざまな抽出法について知っておくことは必須ではありません。分析者側が抽出法について知らなくても問題ないような工夫（Replication Method）が施されているからです。そして，いずれの抽出法を使用しているにせよ，標本から母集団を推定する方法は，基本的にはSRSの条件下での推定の拡張です。

そこで以下では，SRSの条件下で，どのように標本から母集団を推定すればよいのか学んでいくことにしましょう。なお，ここで留意すべきは，これから学ぶ方法はあくまでも「SRSの条件下」であるという点です。すでに述べたように，LSAでSRSが採用されることはほぼありません。ですから，SRSの方法をそのまま母集団の推定に当てはめることは，ときに誤った推測に繋がります。 SRSの理屈は学びつつ，「どこがLSAに適用できて，どこが適用できないのか」という点を意識しておくことが重要なのです。

4.3 変数という考え方

続いて「変数」という考え方について説明します。社会調査では，さまざまな質問をします。このとき個々の設問への回答は，変数という形でまとめられます。「朝ごはん」変数とか，「国語の学力」変数といった具合です。変わる数だから変数と覚えておけばいいでしょう³。

変数にはいくつか種類がありますが，大雑把には，足し算・引き算ができる変数（量的変数）と足し算・引き算のできない変数（質的変数）の2種類があると思っておけば十分です。

前者の代表は，学力テストの点数です。国語の成績と算数の成績を足して2で割って平均を求めるといった作業が想定できます。また，「女子の国語の点数が70点，男子の国語の点数は60点だから，女子の方が10点成績がよい」といった引き算をすることも可能です。

後者の代表は，よくあるアンケートの回答を想像すればいいでしょう。たとえば「朝ごはんを食べますか？」という質問に対する，「1:はい」「2:いいえ」といった回答です。ここではアンケートの回答に1や2といった数値を当てはめていますが，これはたまたまそう設定しただけで，「1:いいえ」「2:はい」でも構いません⁴。また，「2:いいえ」から「1:はい」を引くと「1:はい」になるといった引き算は（できなくはないですが），実質的な意味はありません。

量的変数と質的変数では，適用できる統計手法が異なります。そのため，自分が扱っている変数がいずれの種類なのか区別しておくことは重要です。 LSAでは学力という量的変数が主な関心の対象になりますから，以下では量的変数に焦点を当て，標本から母集団を推定する方法を解説します。

4.4 平均

よく使われる統計量の代表が，平均です。 \(x_1\), \(x_2\)，・・・，\(x_i\)，・・・\(x_n\)の\(n\)個のデータに対して，その平均\(\mu\)は以下の式で定義されます。

\[\mu = \frac{1}{n}\sum_{i=1}^nx_i\]

数学記号が出てきて驚くかもしれませんが，要は「データをすべて足して，データの数で割る」ということです。 Rでは，オブジェクトに対してさまざまな操作をするコマンド（これを「関数」と呼びます）が用意されています。たとえばベクトルの要素をすべて足す場合はsum関数が使えますし，ベクトルの要素の数はlength関数で取得できます。また，ベクトルの平均を計算するmean関数も用意されています。

ここでは簡単のため，児童数5人の学級AとBがあると考えます。 Aクラスの5人の成績は，40点・40点・60点・80点・80点です。 Bクラスの5人の成績は，20点・20点・60点・100点・100点とします。このとき，それぞれの平均（どちらも60点になります）は Rで以下のように計算できます。

# Aクラスのベクトルを作成
A <- c(40, 40, 60, 80, 80)
# Bクラスのベクトルを作成
B <- c(20, 20, 60, 100, 100)
sum(A) / length(A) # Aの数値をすべて合計し，要素数（5）で割る

[1] 60

mean(B) # mean関数が用意されている

[1] 60

4.5 分散

さて，AクラスもBクラスも平均は60点ですが，両者は点数のばらつき具合が違います。 Aクラスは最小値40点・最大値80点に対し， Bクラスは最小値20点・最大値100点なので，成績のばらつきは明らかにBクラスのほうが大きくなっています。

こうしたデータのばらつきを表す統計量が分散です。分散は，次の式で計算します。

\[\frac{1}{n}\sum_{i=1}^n(x_i - \mu)^2\]

数式では難しいかもしれないので，Rで考えてみましょう。データのばらつきを表現する際に手っ取り早いのは，すべての要素から平均を引いてしまうことです。 Rで表現すると，次のようになります。

A - mean(A)

[1] -20 -20   0  20  20

B - mean(B)

[1] -40 -40   0  40  40

この結果を見ると，最小値-20・最大値20のAクラスより，最小値-40・最大値40のBクラスの方がばらつきが大きいことは明らかです。ただ，今回は要素が5つと少ないのでまだ良いのですが，要素の数が多くなると全体を把握することは困難になります。そこで，得られた結果を1つの値にまとめることを考えましょう。手っ取り早いのは，sum関数を使って全部足してしまうことです。

sum(A - mean(A))

[1] 0

sum(B - mean(B))

[1] 0

0になってしまいました。プラスとマイナスの数値があるので，相殺して0になってしまうのです。どうすればいいのでしょうか。

こういう場合に統計学でよく使われる方法が，要素を全部2乗してしまうというものです。 2乗すればマイナス×マイナスはプラスということで，すべての値が正になります。 Rの場合，Aというベクトルの要素をすべて2乗したければ， A^2と書くだけで十分です。今回は，A - mean(A)を2乗しなければならないので， (A - mean(A))^2とした後に，その合計（sum）を計算します。混乱するかもしれませんが，以下のように少しずつコードを増やしていけば大丈夫です。

A # Aクラスの成績

[1] 40 40 60 80 80

A - mean(A) # 平均を引く

[1] -20 -20   0  20  20

(A - mean(A))^2 # 要素を2乗

[1] 400 400   0 400 400

sum((A - mean(A))^2) # 合計を計算

[1] 1600

sum((B - mean(B))^2) # Bクラスについても同じ処理

[1] 6400

こうすることで，AよりBの方がばらつきが大きいということが， 1つの数値で表現できます⁵。

ただ，この数値にも問題があります。それは，要素の数が倍になるとデータのばらつきが変わっていないのに数値が大きくなってしまうという問題です。今，Aが二つ合体したA2というベクトルを考えましょう。

A2 <- c(A, A)
sum((A2 - mean(A2))^2)

[1] 3200

A2はAが二つくっついただけなので，ばらつきは変わらないはずですが，計算結果は1600から3200と2倍になっています。これは困るということで，最後に要素数\(n\)で割ります。

(sum((A - mean(A))^2)) / length(A)

[1] 320

(sum((B - mean(B))^2)) / length(B)

[1] 1280

(sum((A2 - mean(A2))^2)) / length(A2)

[1] 320

AよりBの方がばらつきが大きく，AとA2のばらつきは同じという結果になりました。この計算が，分散の式で行われていることです。

4.6 分散をRの関数にまとめる

ところで，毎回(sum((A - mean(A))^ 2)) / length(A)を入力するのは大変です。 Aを入力するところが3箇所もあるので，そのうち間違えそうな気がします。そこでRの関数を自作することを考えます。最初はなかなかピンとこないと思いますが，慣れると複雑な処理をひとまとめにして繰り返し使うことができるので，大変便利な操作です。

関数を自作する場合，functionという関数を使います。先ほどの分散をまとめる処理を，新しくVARという関数にすることを考えましょう。以下のように書くと，VARという関数を登録することができます。

VAR <- function(x) {
  (sum((x - mean(x))^2)) / length(x) # 関数の処理を書く
}

VAR(A)

[1] 320

VAR(B)

[1] 1280

VAR(A2)

[1] 320

ちなみにRにも分散を求める関数varが用意されています。ただ，このvarは先ほど作ったVARとは違う結果を返します。

var(A)

[1] 400

var(B)

[1] 1600

var(A2)

[1] 355.5556

これはVARが間違っているというわけではありません。標本から母集団の分散を推定する場合，その式は，次のようになります。

\[\frac{1}{n-1}\sum_{i=1}^n(x_i - \mu)^2\]

違いは\(n\)ではなく，\(n-1\)で割っているという点です。詳しい説明は省きますが，こちらの式の方が母集団の分散を適切に推定できることがわかっています。 Rに用意されているvarは，この式を実装したものです。そのため，varで計算した値に，\(\frac{n-1}{n}\)をかけると， VARの値と一致します。

var(A) * (length(A) - 1) / length(A)

[1] 320

var(B) * (length(B) - 1) / length(B)

[1] 1280

var(A2) * (length(A2) - 1) / length(A2)

[1] 320

4.7 標準偏差

先ほど計算した分散は，都合上，途中で数値を2乗していました。そのため，もとのデータと比べると単位がズレています⁶。ここで，分散の平方根を取ると，単位が揃います。これを標準偏差と呼びます。次の章で扱いますが，標準偏差はいろいろと便利な性質を持つので，よく使われます。

なお分散と同じく，標本の分散VARなのか，標本から母集団を推定した分散varなのかによって，標準偏差も微妙に値が変わります。

sqrt(VAR(A))

[1] 17.88854

sqrt(VAR(B))

[1] 35.77709

sqrt(VAR(A2))

[1] 17.88854

sqrt(var(A))

[1] 20

sqrt(var(B))

[1] 40

sqrt(var(A2))

[1] 18.85618

Rには，母集団の標準偏差を推定するための関数sdが用意されています。これは，sqrt(var(x))と同じ値を返します。

sd(A)

[1] 20

sd(B)

[1] 40

sd(A2)

[1] 18.85618

4.8 最大値・最小値・中央値

平均・分散・標準偏差以外に登場するものとして，最大値，最小値，中央値といった値があります。中央値は，データを順に並べたときの真ん中の値のことです。もし真ん中の値が二つある場合は，その平均が中央値になります。ちなみに，データを順に並べたときに前から\(\frac{1}{4}\)を第1四分位，前から\(\frac{3}{4}\)を第3四分位と呼びます。

Rでは，summary関数を使って，これらの値を計算することができます。また，median，max，minといった関数を使うことでも算出できます。

x <- c(30, 40, 50, 60, 70)
summary(x) # Min:最小値，1st Qu:第1四分位，Median:中央値，3rd Qu:第3四分位，Max:最大値

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
     30      40      50      50      60      70

max(x) # 最大値

[1] 70

min(x) # 最小値

[1] 30

median(x) # 中央値

[1] 50

平均や分散については，後半で説明します。↩︎
令和3年度の抽出法について，国立教育政策研究所のウェブサイトに資料が載っています。↩︎
厄介なことに，Rのオブジェクトも「変数」と呼ぶことがあります。混乱すると思うので，本書でRの説明をするときは「変数」という言葉を使っていません。↩︎
アンケートの回答は，数値にして管理することが一般的です。もし「はい」「いいえ」といった文字のまま管理したら，打ち間違いが発生する危険があります（コンピュータは融通がききませんので，「はい」「はぃ」「ハイ」はすべて違う意味になります）。また，回答が長い場合（たとえば「いつもある」「ときどきある」「あまりない」「まったくない」など），分析時に非常に扱いづらくなります。↩︎
この辺まで来るとベクトルのありがたさがわかるようになります。この計算をベクトルを使わずやろうと思うと， sum(((40 - 60)^2 + (40 - 60)^2 + (60 - 60)^2 + (80 - 60)^2 + (80 - 60)^2)) となってしまいます。今は要素が5つですからなんとか計算できますが，要素が1000や2000になったらもう手に終えません。ベクトルを使えば，Aの要素が1000になっても2000になっても， sum((A - mean(A))^2)は変わらないのです。↩︎
仮にもとの単位が\(m\)（メートル）だったとすると，途中で2乗しているので\(m^2\)（平方メートル）になっています。↩︎